Vídeo: Quina és la complexitat de l'algorisme d'ordenació de pila?
2024 Autora: Lynn Donovan | [email protected]. Última modificació: 2023-12-15 23:44
L'ordenació de pila és un algorisme in situ. Temps Complexitat : Complexitat temporal de heapify és O(Logn). Complexitat temporal de createAndBuildHeap() és O(n) i en general complexitat temporal de Heap Sort és O(nLogn).
Respecte a això, quin és l'algorisme d'ordenació de pila?
Algorisme d'ordenació de pila es divideix en dues parts bàsiques: Creació a Munt de la llista/matriu sense ordenar. Llavors a ordenat La matriu es crea eliminant repetidament l'element més gran/menor del fitxer Munt , i inserint-lo a la matriu. El Munt es reconstrueix després de cada retirada.
De la mateixa manera, quin és el temps d'execució típic d'un algorisme d'ordenació de pila? Tanmateix, quicksort té el pitjor dels casos temps d'execució de O (n 2) O (n ^ 2) O (n2) i una complexitat espacial en el pitjor cas de O (log ? n O (log n O (logn), per tant, si és molt important tenir un cas pitjor ràpid). temps d'execució i ús eficient de l'espai, heapsort és la millor opció.
De la mateixa manera, es pregunta, quina és la complexitat de la funció Heapify?
La idea principal és que al build_heap algorisme l'actual amuntegar el cost no és O(log n) per a tots els elements. Quan amuntegar s'anomena, el temps d'execució depèn de com es pot moure l'element cap avall a l'arbre abans que finalitzi el procés. En altres paraules, depèn de l'alçada de l'element al munt.
Quin algorisme d'ordenació té millor complexitat asimptòtica?
Per El millor Inserció de cas Ordena i Heap La classificació és la millor un com els seus millor temps d'execució del cas complexitat és O(n). Per al cas mitjà millor asimptòtic temps d'execució complexitat és O(nlogn) que ve donada per Merge Ordena , Munt Ordena , Ràpid Ordena . Per al pitjor dels casos millor temps d'execució complexitat és O(nlogn) que ve donat per Merge Ordena , Munt Ordena.
Recomanat:
Quin algorisme d'ordenació té millor complexitat asimptòtica?
Ordenació de pila
Quin algorisme d'ordenació és millor en el pitjor dels casos?
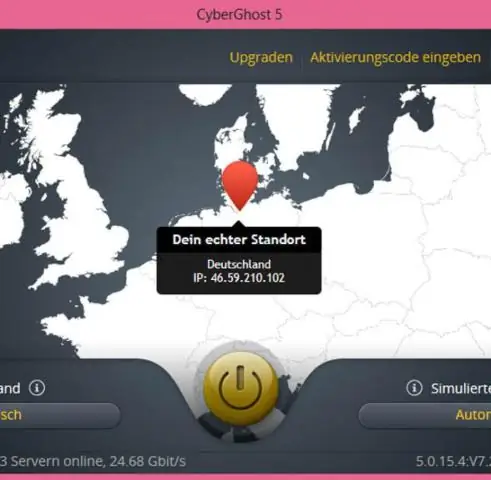
Algoritmes d'ordenació Algorisme Estructura de dades Complexitat temporal:Pitjor Ordenació ràpida Matriu O(n2) Ordenació combinada Matriu O(n log(n)) Ordenació munt Array O(n log(n)) Ordenació suau Matriu O(n log(n))
Com es calcula la complexitat de l'ordenació de la combinació?
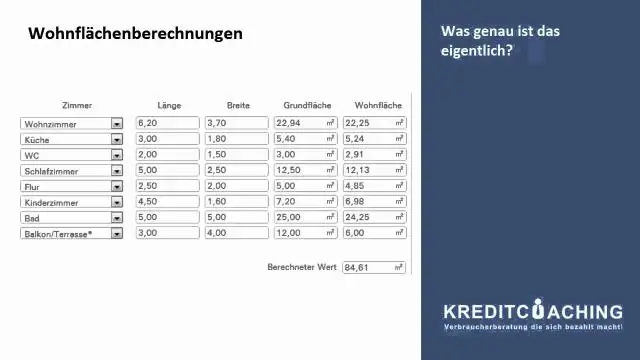
2 respostes. La divisió d'un node A[L,R] en dos nodes requereix R−L+1 temps i després fusionar els dos nodes fills A[L,M] i A[M+1,R] torna a prendre A[R−L +1] temps. Així, per a cada node, el nombre d'operacions que realitza l'algorisme és igual al doble de la mida de la matriu corresponent a aquest node
Quina és la complexitat temporal de l'operació de push de la pila?
Per a totes les operacions de pila estàndard (push, pop, isEmpty, size), la complexitat del temps d'execució en el pitjor dels casos pot ser O(1). Diem que es pot i no és perquè sempre és possible implementar piles amb una representació subjacent que és ineficient
Quina és la millor complexitat de temps de cas de l'ordenació de combinació?
Algoritmes d'ordenació Algoritme Estructura de dades Complexitat espacial:Pitjor Ordenació ràpida Matriu O(n) Ordenació combinada Matriu O(n) Ordenació munt Array O(1) Ordenació suau Matriu O(1)