Vídeo: Què és la primera cerca en amplitud i la primera cerca en profunditat?
2024 Autora: Lynn Donovan | [email protected]. Última modificació: 2023-12-15 23:44
BFS significa Primera recerca d'amplada . DFS significa Primera recerca en profunditat . 2. BFS ( Primera recerca d'amplada ) utilitza l'estructura de dades de la cua per trobar el camí més curt. BFS pot ser utilitzat trobar camí més curt d'una sola font en un gràfic no ponderat, perquè en BFS , arribem a un vèrtex amb un nombre mínim d'arestes des d'un vèrtex font.
D'aquí, què és la primera cerca en profunditat amb exemple?
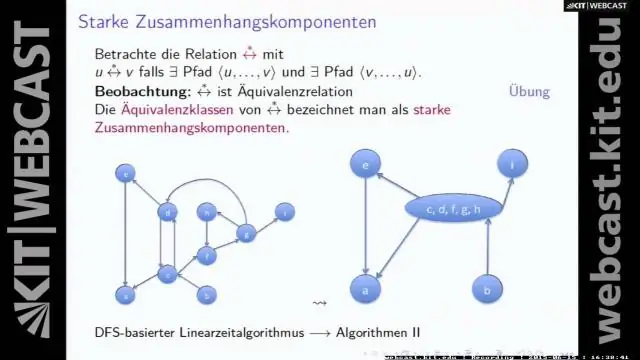
Primera recerca en profunditat o DFS per a un gràfic. Primer recorregut de profunditat (o Cerca ) per a un gràfic és semblant a Primer recorregut de profunditat d'un arbre. Per exemple , en el gràfic següent, comencem travessa del vèrtex 2. Quan arribem al vèrtex 0, nosaltres mira per a tots els seus vèrtexs adjacents. 2 també és un vèrtex adjacent de 0.
Al costat de dalt, què retorna la primera cerca de profunditat? El profunditat - primera recerca L'algorisme ens permet determinar si dos nodes, el node x i el node y, tenen un camí entre ells. L'algorisme DFS fa això mirant tots els fills del node inicial, el node x, fins que arriba al node y.
De la mateixa manera, què és la primera cerca ampla?
Primera recerca d'amplada (BFS) Algorisme Primera recerca d'amplada és un gràfic travessa algorisme que comença a recórrer el gràfic des del node arrel i explora tots els nodes veïns. A continuació, selecciona el node més proper i explora tots els nodes inexplorats.
Per a què serveix la primera cerca en profunditat?
profunditat - primera recerca s'utilitza en l'ordenació topològica, la planificació de problemes, la detecció de cicles en gràfics i la resolució de trencaclosques amb una sola solució, com ara un laberint o un sudoku. Altres aplicacions impliquen l'anàlisi de xarxes, per exemple, provar si un gràfic és bipartit.
Recomanat:
La cerca lineal és el mateix que la cerca seqüencial?
Classe: algorisme de cerca
Quina és la millor primera cerca cobdiciosa en intel·ligència artificial?
Algoritme de cerca del millor primer (Greedy Search): l'algoritme de cerca del millor primer primer sempre selecciona el camí que apareix millor en aquell moment. En el millor primer algorisme de cerca, expandim el node més proper al node objectiu i el cost més proper s'estima mitjançant la funció heurística, és a dir, f(n)= g(n)
Què és la primera cerca ampla en intel·ligència artificial?
Publicat el 4 d'abril de 2017. La cerca ample és com recórrer un arbre on cada node és un estat que pot ser un candidat potencial per a la solució. Expandeix els nodes des de l'arrel de l'arbre i després genera un nivell de l'arbre alhora fins que es troba una solució
Què és la profunditat del processament en psicologia?
Per "profunditat de processament", ens referim a la manera com una persona pensa sobre una informació, per exemple, un nivell poc profund de processament d'una paraula seria passar una estona per sobre d'una frase i entendre-la sense detenir-se en el paraula individual
Quin cas posa en majúscula la primera lletra de la primera paraula de cada frase?
La casella de selecció Posa en majúscula la primera lletra de les frases està seleccionada de manera predeterminada. Quan està seleccionat, Visio majúscules la primera lletra de qualsevol paraula que segueix un punt, un retorn de carro, un punt i coma o la primera lletra de qualsevol paraula en una llista o columna de taula